Obične diferencijalne jednačine drugog reda

Metodi resavanja najpoznatijih tipova obicnih diferencijalnih jednacina drugog reda.

2.1 Slučaj svođenja na jednačinu prvog reda

Opšta diferencijalna jednačina drugog reda ima oblik:

U nekim slučajevima jednačina može se svesti na diferencijalnu jednačinu prvog reda.

1)

Pomoću smene ova jednačina se svodi na jednačinu prvog reda oblika:

.

2)

Za rešavanje ovakve jednačine treba koristiti smenu. Tada se dobija . Tada polazna jednačina postaje jednačina prvog reda:

2.2 Homogena linearna diferencijalna jednačina drugog reda sa konstantnim koeficijentima

Rešenje jednačine treba tražiti u obliku , gde je l konstanta. Odavde se dobija 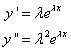pa jednačina dobija oblik::

Dakle, je rešenje jednačine ako lzadovoljava tzv. karakterističnu jednačinu .

Moguća su tri slučaja:

1⁰) tada su 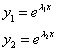linearno nezavisna rešenja jednačine pa je opšte rešenje jednačine dato sa:

gde su C1 i C2 proizvoljne konstante.

2⁰) tada je (). Na osnovu prethodnog slučaja rešenje jednačine može se izraziti u obliku:

Pošto je rešenje može se transformisati u sledeći oblik:

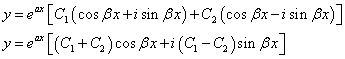
gde su A i B proizvoljne konstante.

3⁰) u ovom slučaju partikularna rešenja 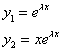jednačine su linearno nezavisna pa opšte rešenje glasi:

2.3 Nehomogena linearna diferencijalna jednačina drugog reda sa konstantnim koeficijentima

Rešenje odgovarajuće homogene jednačine, oblika , može se uvek odrediti pa se uvek može odrediti i rešenje jednačine . U opštem slučaju za rešavanje ove jednačine koristi se metod varijacije konstanata, ali za neke specijalne oblike funkcije h(x) taj metod se može izbeći:

1⁰)

Ako je partikularno rešenje jednačine treba tražiti u obliku polinoma:

Koeficijenti polinoma polinoma dobijaju se metodom neodređenih koeficijenata.

Ako je partikularno rešenje treba tražiti u obliku:

Za rešenje jednačine dobija se direktnom integracijom.

Metod neodređenih koeficijenata

Naći sve izvode rešenja :

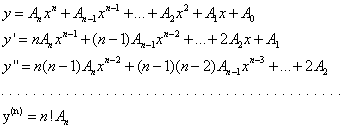
Sve dobijene izvode vratiti u jednačinu a zatim izjednačiti koeficijente uz odgovarajuće članove.

2⁰)

U zavisnosti od rešenja karakteristične jednačine:

partikularno rešenje treba tražiti u obliku:

a)

b)

c)

gde je K privremeno neodređena konstanta.

3⁰)

Ako ip nije koren karakteristične jednačine partikularno rešenje treba tražiti u obliku:

a ako jeste, onda rešenje tražiti u obliku:

4⁰) , gde je Pn(x) polinom n-tog stepena

Ako a nije rešenje karakteristične jednačine tada je , gde je Qn(x) polinom n-tog stepena sa neodređenim koeficijentima. Ako je a rešenje jednačine onda je , gde je r višestrukost rešenja a ().

5⁰)

Ako nije rešenje karakteristične jednačine uzeti:

gde su SN(x) i TN(x) polinomi stepena .

U suprotnom slučaju, ako je rešenje karakteristične jednačine onda je:

gde je r višestrukost rešenja (za jednačine drugog reda ).

2.4    Ojlerova linearna jednačina drugog reda

Prvo treba rešiti odgovarajuću homogenu jednačinu:

Ako se pretpostavi da jednačina ima rešenje oblika ( je parametar koji treba odrediti) tada je 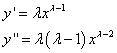pa jednačina postaje:

Razlikuje se nekoliko slučajeva:

1⁰)

Opšte rešenje jednačine glasi:

gde su C1 i C2 proizvoljne konstante.

2⁰)

U ovom slučaju, iz

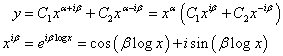
dobija se opšte rešenje jednačine u obliku:

gde su A1 i A2 proizvoljne konstante.

3⁰)

U ovom slučaju partikularna rešenja jednačine su i pa opšte rešenje glasi:

gde su C1 i C2 proizvoljne konstante.

U sva tri slučaja prećutno je pretpostavljeno da je . Ako je treba poći od rešenja oblika .

Opšte rešenje nehomogene jednačine dobija se iz opšteg rešenja homogene jednačine standardnim metodom varijacije
konstanata.

Series Navigation

Diferencijalne jednacine prvog redaDiferencijalne jednačine (PDF & TeX)