- Diferencijalne jednacine prvog reda
- Obične diferencijalne jednačine drugog reda
- Diferencijalne jednačine (PDF & TeX)
Kratak pregled metoda resavanja najpoznatijih tipova obicnih diferencijalnih jednacina prvog reda
1.1 Razdvojene promenljive
![]()
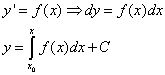
U opštem slučaju:
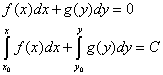
1.2 Homogena diferencijalna jednačina
![]()
Smenom: ![]() polazna jednačina postaje:
polazna jednačina postaje:
![]()
tj. diferencijalna jednačina oblika
Primedba: diferencijalna jednačina oblika:
![]()
gde je a, b, c, A, B, C = const, može se svesti na jednačinu oblika . Moguća su dva slučaja:
1o) Ako je ![]() smenom:
smenom: ![]() jednačina postaje:
jednačina postaje:
![]()
Sistem jednačina:
![]()
ima rešenje po a i bpa jednačina postaje:
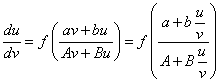
a to je jednačina oblika .
20) Neka je ![]() , tj.
, tj. ![]() gde je k konstanta. Smenom
gde je k konstanta. Smenom ![]() , gde je u nova nepoznata f-ja promenljive x. Jednačina postaje:
, gde je u nova nepoznata f-ja promenljive x. Jednačina postaje:
![]()
odnosno jednačina oblika .
1.3 Linearna diferencijalna jednačina
![]()
Ako je ![]() jednačina se naziva homogena linearna diferencijalna jednačina.
jednačina se naziva homogena linearna diferencijalna jednačina.
1o) Homogena jednačina:
![]()
za ![]() postaje:
postaje:
![]()
tj. jednačina oblika čije je rešenje:
![]()
Može se uzeti ![]() kao rešenje jednačine .
kao rešenje jednačine .
2o) Da bi rešili pretpostavimo ![]() :
:
![]()
![]()
ako se jn-e i zamene u dobija se:
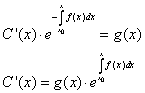
odnosno:
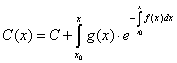
pa je opšte rešenje jednačine :
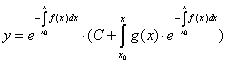
U eksplicitnom obliku opšte rešenje jednačine dato je kao:
![]()
tj. rešenje je izraženo kao linearna funkcija integracione konstante.
1.4 Bernulijeva jednačina
![]()
Gde je ![]() , za
, za ![]() jednačina postaje linearna.
jednačina postaje linearna.
Uvođenjem smene 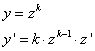 , gde je z nova nepoznata f-ja a k konstanta, jednačina postaje:
, gde je z nova nepoznata f-ja a k konstanta, jednačina postaje:
![]()
![]()
Konstantu k treba izabrati tako da je:
![]()
Posle ove smene jednačina glasi:
![]()
a to je linearna jednačina. Opšte rešenje ove jednačine ima oblik:
![]()
Prema tome, opšte rešenje Bernulijeve jednačine može se izraziti u eksplicitnom obliku:
![]()
1.5 Rikartijeva jednačina
![]()
Za ![]() jednačina postaje Bernulijeva jednačina , odnosno linearna jednačina . U opštem slučaju jednačina se ne može rešiti.
jednačina postaje Bernulijeva jednačina , odnosno linearna jednačina . U opštem slučaju jednačina se ne može rešiti.
Ako je poznato jedno partikularno rešenje može se dobiti i opšte rešenje jednačine .
Smenom ![]() , gde je y1(x) jedno partikularno rešenje a z nova nepoznata funkcija jednačina postaje:
, gde je y1(x) jedno partikularno rešenje a z nova nepoznata funkcija jednačina postaje:
![]()
![]()
a to je linearna jednačina. Opšte rešenje ove jednačine ima oblik:
![]()
Prema tome opšte rešenje Rikartijeve jednačine ima oblik:
![]()
gde je C proizvoljna konstanta a F, G, H i K određene funkcije.
1.6 Klerova jednačina
![]()
Smenom ![]() jednačina postaje:
jednačina postaje:
![]()
odakle se, nakon diferenciranja po x, dobija:
![]()
10) Ako je ![]() pa na osnovu jednačine opšte rešenje jednačine ima oblik:
pa na osnovu jednačine opšte rešenje jednačine ima oblik:
![]()
2o) Ako je ![]() eliminacijom p iz jednačina
eliminacijom p iz jednačina ![]() dobija se singularno rešenje jednačine koje nije izraženo u opštem rešenju.
dobija se singularno rešenje jednačine koje nije izraženo u opštem rešenju.
1.7 Lagranževa jednačina
![]()
Ova jednačina se rešava slično kao i Klerova. Posle smene ![]() jednačina dobija oblik:
jednačina dobija oblik:
![]()
odakle se, nakon diferenciranja, dobija:
![]()
![]()
Ako je ![]() jednačina je Klerova, pretpostavimo onda da je
jednačina je Klerova, pretpostavimo onda da je ![]() tada jednačina postaje:
tada jednačina postaje:
![]()
a to je linearna jednačina. Jednačina ima rešenje oblika
![]()
pa je opšte rešenje Lagranževe jednačine u parametarskom obliku:
![]()
1.8 Jednačina prvog reda drugog stepena
![]()
Ako se jednačina može napisati u obliku:
![]()
tada se rešavanje jednačine svodi na rešavanje dve jednačine prvog stepena:
![]()
Opšta rešenja ovih jednačina su ![]() pa je opšte rešenje jednačine :
pa je opšte rešenje jednačine :
![]()
gde je C proizvoljna konstanta.
1.9 Totalni diferencijal
![]()
gde funkcije P i Q imaju neprekidne parcijalne izvode po x i z. Ako postoji funkcija u(x,y) takva da važi:
![]()
tada se jednačina naziva jednačina sa totalnim diferencijalom, ili egzaktna diferencijalna jednačina..
Opšte rešenje egzaktne diferencijalne jednačine određeno je relacijom:
![]()
gde je C proizvoljna konstanta.
Da bi se odredila funkcija u, za koju važi , treba poći od jednakosti:
![]()
odakle se, upoređivanjem sa dobija:
![]()
odnosno:
![]()
Ovi mešoviti izvodi su po pretpostavci neprekidni pa su i jednaki, pa je, prema tome, ![]() potreban uslov da jednačina bude sa totalnim diferencijalom.
potreban uslov da jednačina bude sa totalnim diferencijalom.
Ako je ovaj uslov ispunjen iz prve jednačine u dobija se:
![]()
gde je f(y) neprekidna funkcija. Diferenciranjem izraza dobija se:
![]()
![]()
Druga jednačina u i jednačina daju:
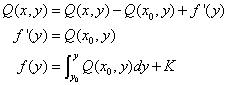
gde je K proizvoljna konstanta.
Konačno se dobija:
![]()
pa je opšte rešenje jednačine dato sa:
![]()
gde je C proizvoljna konstanta.




![Pomračenje Meseca polusenkom (5. maj 2023) 4 Slika dana: Mesec u polusenci [18.10.2013]](https://i0.wp.com/www.svetnauke.org/wp-content/uploads/2013/10/2013-10-18-Mesec-u-polusenci1.jpeg?fit=2000%2C1600&ssl=1)





![Prvi teleskop 10 Slika dana: Galileo Galilej i teleskop [25.08.2014]](https://i0.wp.com/www.svetnauke.org/wp-content/uploads/2014/08/2014-08-25-Galileo-Galilej-i-teleskop.jpg?fit=800%2C595&ssl=1)















zastrasujuce 😀 ja sam samo mala pravnica u svetu opasnih fizicara 😉
Hehehe, pa nije toliko strasno 🙂 Bar ne kao ti vasi zakoni i crne rupe u njima 😀
sve je stvar ukusa, a ukusi se razlikuju 😀
vrlo dobro!
zasto nema Lagranzova jed druge vrste….shmrc
Zato sto je to jednacina drugog reda. U planu je da napisem nesto i o nekim najpoznatijim j-nama drugog reda, kao i specijalnim funkcijama ali… sve je jos samo na papirima…
ajde molim te maskiraj se i izadji na ispit umesto mene 🙂
gore si na pisao u homogenim jednachinama
"jednachina postaje
(pa slika)
odnosno jednachina oblika"
jel to to ili si izostavio tekst posle ovog "oblika"
Treba da stoji oznaka jednačine, ali nestalo je u konverziji.
Rečenica treba da glasi:
odnosno jednačina oblika y'(x) = f(x).
Pozdrav Milane,
da li si razmisljao da neke svoje clanke (npr ovo o dif. jednacinama) publikujes na http://sr.wikipedia.org ?
Mislim da bi tvoji clanci bili pravo osvezenje!
Da, razmišljao sam više puta o tome ali nekako uvek na tome i ostane. Ima dosta posla oko ubacivanja članaka, tako da… možda jednog dana 🙂
zasto je resenje j-ne sa totalnim dif. dato u tom obliku
mozes li da analiziras to resenje
Ne razumem pitanje?
@Milan Milošević
Mozes li to resenje da uporedis sa resenjem Rikatijeve j-ne .Kod Rikatijeve ako imamo dva partikularna resenja sve vreme radimo sa y kao da je poznato i tek na kraju ga izvucemo ispred i tu je opste resenje dato u f-ji x i C sto opste resenje i jeste u opstem obliku- f-ja od x i C. Jel bi mozda trebalo da se kaze da je kod totalnog dif. opste resenje u f-ji od x i C jer y koje figurise u opstem resenju je takodje f-ja od x i C?
Da nemas mozda gresku u opstem resenju nehomogene linearne diferencijalne jednacine? Jedan znak – ti je visak u zagradi… Proveri na http://www.rgf.bg.ac.rs/predmet/RO/II%20semestar/…/M2_RO_DJ.pdf
Pozzz